How to convert a complex number to polar form and back

There are three very common ways of writing any complex number z:

Standard form: z = x + i y
Polar form: z = |z| (cosφ + i sinφ)
Exponential form: z = |z| e^iφ

In this post we explain how to get from any of these representations to the other ones.

From standard form to polar form and back

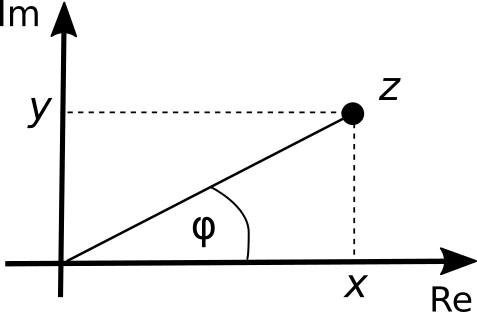
We begin with a complex number in standard form z = x + i y. Here x and y are real numbers. The number x is called the real part and y is called the imaginary part of z. If we consider the numbers x and y to be coordinates of a point (x,y) in the plane, then this point represents the number z. In this way, any complex number can be plotted as a point. We call the axis of x the real axis and the axis of y the imaginary axis. So the two-dimensional plane with two real coordinates, called complex plane, represents the set of all complex numbers

A point representing the number z in the complex plane

$\mathbb{C}=\{x+iy \left| x,y \in \mathbb{R} \right. \}$ .

After plotting the number z in the complex plane, we can define two meaningful quantities:

The absolute value |z|: This is the distance between the point z and the origin of the coordinate system.
The polar angle φ: This is the angle which the line between the origin and the point z forms with the positive real axis.

The absolute value |z| is obtained as:

$\left| z \right| =\sqrt{x^2+y^2} .$

Furthermore, from the usual relations for sine and cosine of an angle in a right-angled triangle, we can read off the following relations between x, y, φ and |z| from the above picture:

$\sin \varphi = \frac{y}{\left| z \right|}, \textrm{ } \cos \varphi = \frac{x}{\left| z \right|}$

If we solve these relations for x and y and insert this into the standard form, we see that the complex number z can be written as

$z=x+iy=\left| z\right| (\cos \varphi +i \sin \varphi ).$

The expression on the right-hand side is the desired polar form of z. Now, as we already have a simple formula for |z|, the last missing ingredient is a formula which lets us compute the polar angle φ for given x and y. From the combination of the above relations involving sine and cosine, we see that we have

$\tan \varphi = \frac{y}{x}$

unless x=0. Let us consider this exception at first. As we can see in the above picture, if x=0, the point z lies somewhere on the imaginary axis. Here we have three possible cases:

If y>0, the point lies on the positive imaginary axis. So the polar angle φ is 90° (i.e. π/2).
If y<0, the point lies on the negative imaginary axis. So the polar angle φ is 270° (i.e. 3π/2).
If y=0, we have z=0. (The polar angle doesn’t matter, because (cosφ + i sinφ) is multiplied with |z|=0.)

In all the other cases where x is different from zero, we use tan φ = y/x to compute φ. We solve for φ and obtain

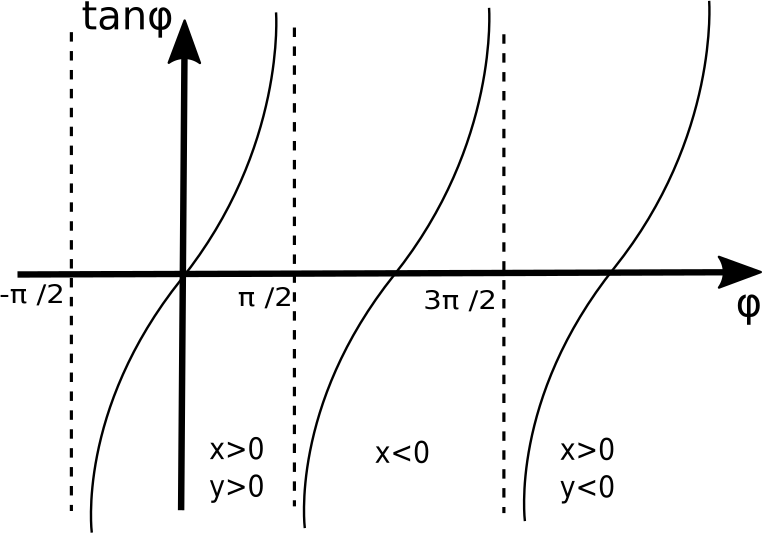
$\varphi=\arctan\frac{y}{x}+k\pi\textrm{ with }k=\begin{cases} 0 & \textrm{for }x>0,y\geq0,\\ 1 & \textrm{for }x<0,\\ 2 & \textrm{for }x>0,y<0. \end{cases}$

It is not surprising that this solution involves the inverse of the tangent, arctan. The additional term kπ comes from the fact that tangent is a π-periodic function with several branches. Depending on the region of the complex plane, different branches apply. For example let’s say the point z is in the left half of the comlex plane, meaning x<0. In this case, the angle φ is somewhere between π/2 (90°) and 3π/2 (270°). (Notice that these two angles are precisely the exceptions corresponding to x=0. Here the tangent function diverges.) As we see in the picture in the right-hand side, the second branch of the tangent applies for this region of the complex plane. So after inverting the first branch and arriving at arctan, we still need to add π in order to arrive at the correct value of φ. This is the case of k=1.

Now that we have computed |z| and φ, we can write z in polar form: z = |z| (cosφ + i sinφ).

Examples

Before we turn to the much easier step to exponential form, let us consider two simple examples for how to derive the polar form. We start with z₁=1+i. The real and the imaginary part of this number are x₁=y₁=1 and we obtain

$\left| z \right| = \sqrt{x_1^2+y_1^2}=\sqrt{2}.$

As we are in the part of the complex plane where real and imaginary part are greater than zero, we are in the case k=0 and arrive at

$\varphi _1 = \arctan \frac{y_1}{x_1}=\arctan 1 = \frac{\pi}{4}.$

In conclusion, we obtain the polar form

$z_1 = \sqrt{2} (\cos \frac{\pi}{4} +i \sin \frac{\pi}{4} ).$

As a second example, we consider z₂=-1+i. The absolute value |z| is again is the square-root of 2. As we have a negative real part x₂=-1, the point is now on the left-hand side of the complex plane, which corresponds to the case k=1. We obtain

$\varphi _2 = \arctan \frac{y_2}{x_2}+\pi=\arctan (-1)+\pi = -\frac{\pi}{4}+\pi=\frac{3}{4}\pi.$

The polar form for z₂ reads

$z_2 = \sqrt{2} (\cos \frac{3}{4}\pi +i \sin \frac{3}{4}\pi ).$

From polar form to exponential form

The step to exponential form is straightforward by the application of Euler’s famous equation

$e^{i \varphi } = \cos \varphi + i \sin \varphi .$

Inserting this relation into the polar form, we arrive directly at

$z = \left| z \right| e^{i \varphi}$

for any complex number. So the only actual work we have to do when converting from one representation to another is to compute |z| and φ from x and y or vice versa. The following box summarizes all the relevant relations for these conversions.